Multivariable calculus extends single-variable calculus to functions of several variables, exploring partial derivatives, multiple integrals, and vector-valued functions. It is fundamental for modeling real-world phenomena in physics, engineering, and economics.
Definition and Importance of Multivariable Calculus
Multivariable calculus is the branch of calculus that deals with functions of multiple variables and their properties. It extends the concepts of single-variable calculus to higher dimensions, enabling the study of partial derivatives, gradients, and multiple integrals. This field is crucial for modeling complex systems in physics, engineering, and economics, where phenomena often depend on multiple variables. Understanding multivariable calculus is essential for solving real-world problems involving optimization, growth, and change in multidimensional spaces.
Overview of Key Concepts in Multivariable Calculus
Multivariable calculus encompasses essential concepts such as functions of several variables, partial derivatives, gradients, and multiple integrals. It introduces vector-valued functions, Jacobian matrices, and the divergence theorem. Key ideas include optimization of multivariable functions, directional derivatives, and the geometric interpretation of level sets. The subject also explores double and triple integrals, surface integrals, and their applications in physics and engineering. These concepts form the foundation for advanced mathematical modeling and problem-solving in diverse scientific fields.

Vectors in Multivariable Calculus
Vectors in multivariable calculus represent quantities with magnitude and direction, enabling operations like addition and scalar multiplication. They form the basis for understanding vector spaces and their applications.

Vector Representation and Operations
Vectors in multivariable calculus are represented as ordered lists of real numbers or geometric entities with magnitude and direction. Operations include addition, subtraction, and scalar multiplication, performed component-wise. The dot product and cross product are essential operations, yielding scalars and vectors, respectively. These operations are fundamental for understanding vector spaces, transformations, and applications in physics, engineering, and economics. Vector representation and operations form the foundation for analyzing complex systems and solving practical problems in higher-dimensional spaces.
Properties of Vectors in R^n
Vectors in R^n possess properties like commutativity and associativity under addition, and distributivity over scalar multiplication. They can be scaled, added, or subtracted, yielding another vector in R^n. The zero vector and unit vectors are fundamental, enabling decomposition of vectors. Norms and orthogonality define vector lengths and angles, crucial for projections and linear independence. These properties underpin vector spaces, facilitating applications in physics, engineering, and economics by allowing the modeling of complex, higher-dimensional systems with precision and clarity.

Functions of Several Variables
Functions of several variables extend single-variable functions, mapping R^n to R. They are essential for modeling complex systems, with applications in physics, engineering, and economics. Their graphical representations and level sets provide insights into their behavior and optimization.
Definition and Classification of Functions
A function of several variables is a mathematical relation between variables that assigns a unique output value to a combination of input values. These functions are classified based on their domain and codomain. Scalar-valued functions map R^n to R, while vector-valued functions map R^n to R^m. Functions can also be categorized as polynomial, rational, exponential, or trigonometric, depending on their form. Classification helps in analyzing their properties, such as continuity, differentiability, and critical points, which are essential for optimization and modeling real-world phenomena.
Graphical Representation and Level Sets
Graphical representation of functions of several variables involves visualizing their behavior in 3D space. For functions of two variables, this often involves plotting surfaces or contour plots. Level sets, or isocontours, represent the set of points where the function equals a constant value. These are particularly useful for understanding the function’s behavior, such as identifying maxima, minima, and saddle points. Level sets are widely applied in fields like geography, economics, and physics to represent phenomena like elevation, temperature, or pressure.

Partial Derivatives
Partial derivatives measure the rate of change of a function with respect to one variable while holding others constant. They are crucial for understanding function behavior and optimization.
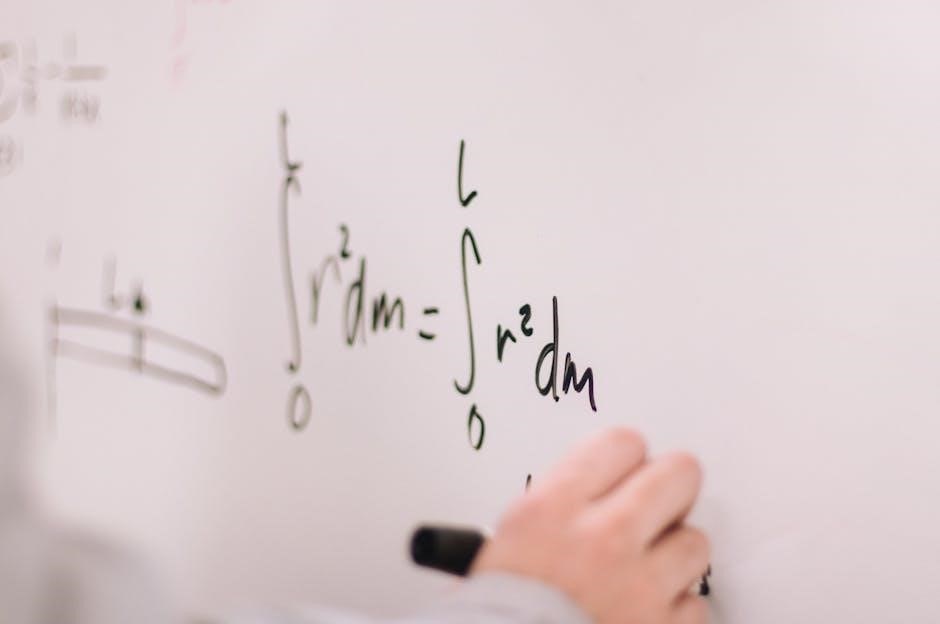
Definition and Computation of Partial Derivatives
A partial derivative of a function measures its rate of change with respect to one variable while keeping others constant. Mathematically, for a function f(x, y), the partial derivative with respect to x is defined as:
∂f/∂x = lim(h→0) [f(x+h, y) ー f(x, y)] / h
Computation involves differentiating with respect to one variable while treating others as constants. This concept extends to higher dimensions, enabling the creation of the gradient vector, which captures all partial derivatives. Partial derivatives are fundamental in optimization and understanding function behavior in multivariable calculus.
Geometric Interpretation of Partial Derivatives
Partial derivatives provide insight into the slope of a function’s graph in specific directions. For f(x, y), ∂f/∂x represents the slope in the x-direction, while ∂f/∂y represents the slope in the y-direction. Geometrically, these derivatives correspond to the tangents of the function’s surface at a given point. The gradient vector, composed of all partial derivatives, points in the direction of steepest ascent, with its magnitude indicating the maximum rate of increase. This interpretation aids in visualizing and analyzing the behavior of multivariable functions in 3D space.

Applications of Partial Derivatives
Partial derivatives are essential in optimizing functions of several variables, crucial in economics for maximizing utility or profit. In physics, they describe gradients like temperature or pressure changes. Engineers use them to model stress in materials or fluid dynamics. Biologists apply partial derivatives to study population growth rates. These derivatives also aid in solving differential equations, which are vital in understanding heat diffusion, wave propagation, and resource allocation. Their versatility makes them a cornerstone in scientific and engineering problem-solving, enabling precise modeling of complex systems.

Multiple Integrals
Multiple integrals extend integration to functions of several variables, enabling the calculation of volumes, areas, and accumulated quantities in higher-dimensional spaces, crucial in physics and engineering.
Double and Triple Integrals
Double and triple integrals extend the concept of integration to two and three variables, respectively. They are used to calculate volumes, surface areas, and solve complex problems in physics and engineering. Double integrals involve integrating a function over a two-dimensional region, while triple integrals extend this to three dimensions. These integrals are evaluated using iterated integrals, where one variable is integrated at a time. They are essential for modeling real-world phenomena, such as electric fields, heat distribution, and fluid flow, making them a cornerstone of multivariable calculus.
Surface Integrals and Their Applications
Surface integrals extend integration to functions defined over curved surfaces, calculating quantities like flux, surface area, and electrical fields. They are evaluated by parameterizing the surface and integrating over two variables. Applications include calculating flux in vector fields, determining surface tension in physics, and solving problems in electromagnetism. Surface integrals are essential tools in engineering and physics for modeling complex systems and understanding interactions across boundaries.
Differential Equations in Multivariable Calculus
Differential equations in multivariable calculus involve rates of change in multiple variables, modeling complex systems in physics, engineering, and biology. They describe interactions and dynamic behavior.

Differential equations in multivariable calculus involve equations that relate functions of several variables to their partial derivatives. These equations model dynamic systems, describing how quantities change over space and time. They are fundamental in understanding complex phenomena in physics, engineering, biology, and economics. Key concepts include partial differential equations, systems of equations, and vector fields. Solving these equations often requires advanced techniques, making them a cornerstone of applied mathematics and scientific modeling. Their applications span fluid dynamics, heat transfer, and population growth, among others.

Solutions and Applications of Differential Equations
Differential equations have diverse solutions, including analytic, numeric, and approximate methods. They model real-world phenomena such as heat diffusion, fluid flow, and population dynamics. In engineering, they optimize systems and design control mechanisms. Applications also extend to economics, biology, and physics, where they describe growth rates, chemical reactions, and wave patterns. Solving these equations provides insights into complex systems, enabling predictions and informed decision-making across various scientific and engineering disciplines. Their versatility makes them indispensable in modern applied mathematics and research.
Applications of Multivariable Calculus
Multivariable calculus is crucial in physics, engineering, and economics, optimizing functions and solving complex systems. It models real-world phenomena, enabling precise predictions and informed decision-making across diverse fields.
Real-World Applications in Physics and Engineering
Multivariable calculus is essential in physics and engineering for modeling complex systems. It enables the analysis of electric fields, fluid dynamics, and heat transfer. Engineers use partial derivatives to optimize structural designs, while physicists rely on multiple integrals to calculate work and energy in multidimensional spaces. Vector calculus, a core component, facilitates the study of forces and motion in three dimensions. These tools are vital for designing advanced technologies, from aerospace systems to medical imaging devices, ensuring precise and efficient solutions to real-world challenges.
Economic and Biological Applications
Multivariable calculus is integral to economic modeling, optimizing profit functions, and analyzing market trends with multiple variables. In biology, it aids in population dynamics, disease spread, and ecological systems. Economists use partial derivatives to study supply-demand equilibrium, while biologists apply differential equations to model growth rates and species interactions. These tools enable precise predictions and informed decision-making in diverse fields, from resource allocation to epidemiology, showcasing the versatility of multivariable calculus in solving real-world problems.
Multivariable calculus is a foundational tool for analyzing complex systems involving multiple variables. It bridges theoretical mathematics with practical applications in physics, engineering, economics, and biology. By mastering concepts like partial derivatives and multiple integrals, students gain the ability to model and solve real-world problems. Its versatility in addressing diverse challenges underscores its importance in modern science and decision-making, making it an essential skill for professionals and researchers seeking to understand and innovate in their fields.
